题目描述:
HDU5462 Manors
n n n个人,每个人 m m m个旗子坐标为 x i , j , y i , j x_{i,j},y_{i,j} xi,j,yi,j, f i ( x , y ) = ∑ j = 1 m ( x − x i , j ) 2 + ( y − y i , j ) 2 f_i(x,y)=\sum_{j=1}^m(x-x_{i,j})^2+(y-y_{i,j})^2 fi(x,y)=∑j=1m(x−xi,j)2+(y−yi,j)2
点 ( x , y ) (x,y) (x,y)被 f i ( x , y ) f_i(x,y) fi(x,y)最小的 i i i 占领, x , y x,y x,y的范围为 [ 0 , 4095 ] [0,4095] [0,4095],求每个人的占领面积。
n ≤ 100 n\le100 n≤100
题目分析:
记 s x i = ∑ j = 1 m x i , j sx_i=\sum_{j=1}^mx_{i,j} sxi=∑j=1mxi,j, s 2 x i = ∑ j = 1 m x i , j 2 s_2x_i=\sum_{j=1}^mx_{i,j}^2 s2xi=∑j=1mxi,j2, y y y同理。
f i ( x , y ) ≤ f j ( x , y ) ⟺ s 2 x i − s 2 x j + s 2 y i − s 2 y j − 2 ( s x i − s x j ) x − 2 ( s y i − s y j ) y ≤ 0 f_i(x,y)\le f_j(x,y)\Longleftrightarrow s_2x_i-s_2x_j+s_2y_i-s_2y_j-2(sx_i-sx_j)x-2(sy_i-sy_j)y\le 0 fi(x,y)≤fj(x,y)⟺s2xi−s2xj+s2yi−s2yj−2(sxi−sxj)x−2(syi−syj)y≤0
相当于对于满足 A x + B y + C ≤ 0 Ax+By+C\le 0 Ax+By+C≤0 的 x , y x,y x,y 有 f i ( x , y ) ≤ f j ( x , y ) f_i(x,y)\le f_j(x,y) fi(x,y)≤fj(x,y)。那么 i i i 的占领面积相当于半平面交。
确定半平面交直线方向向量的方法:
在直线的法向量
(
A
,
B
)
(A,B)
(A,B) 一边的点一定满足
A
x
′
+
B
y
′
+
C
>
0
Ax'+By'+C>0
Ax′+By′+C>0
(对于任意点
x
,
y
x,y
x,y满足
A
x
+
B
y
+
C
=
0
Ax+By+C=0
Ax+By+C=0,有
A
(
x
+
A
)
+
B
(
x
+
B
)
+
C
>
0
A(x+A)+B(x+B)+C>0
A(x+A)+B(x+B)+C>0)
如果令半平面交取左手边(逆时针),那么 < 0 <0 <0 对应的方向向量就是法向量逆时针转 90 ° 90\degree 90°,即 ( − B , A ) (-B,A) (−B,A)
然后再解出一个满足 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0的 ( x , y ) (x,y) (x,y) 就可以确定这条直线了。
半平面交一次转超过 180 ° 180\degree 180°随便举反例,要在外面框个矩形,每次最多转 90 ° 90\degree 90°,最后少于3条线就无解。
举几个例子加深理解:
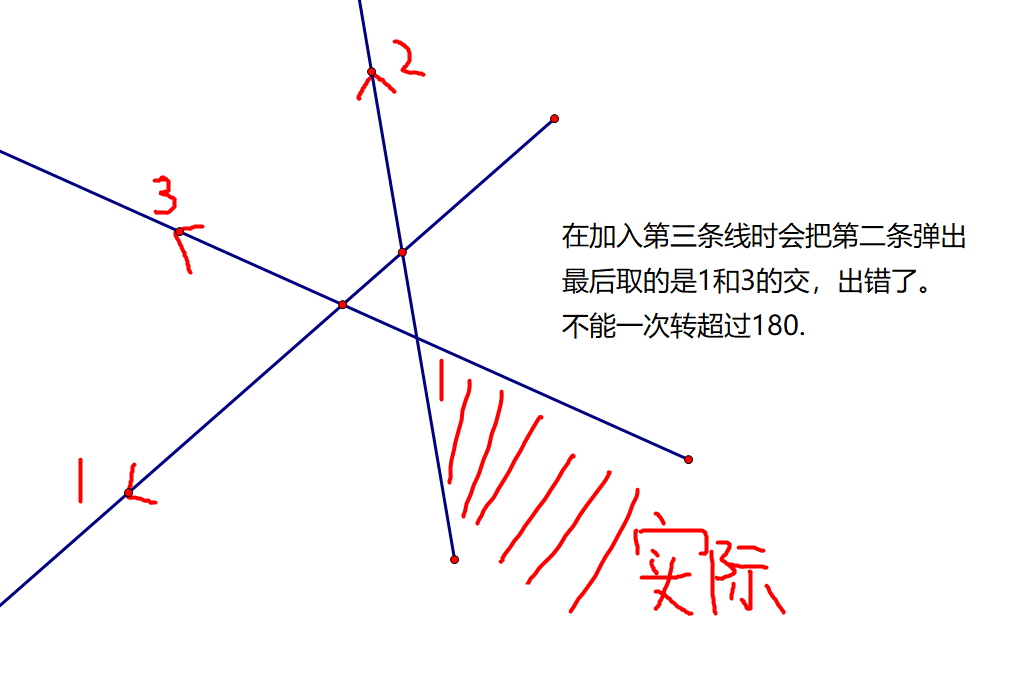
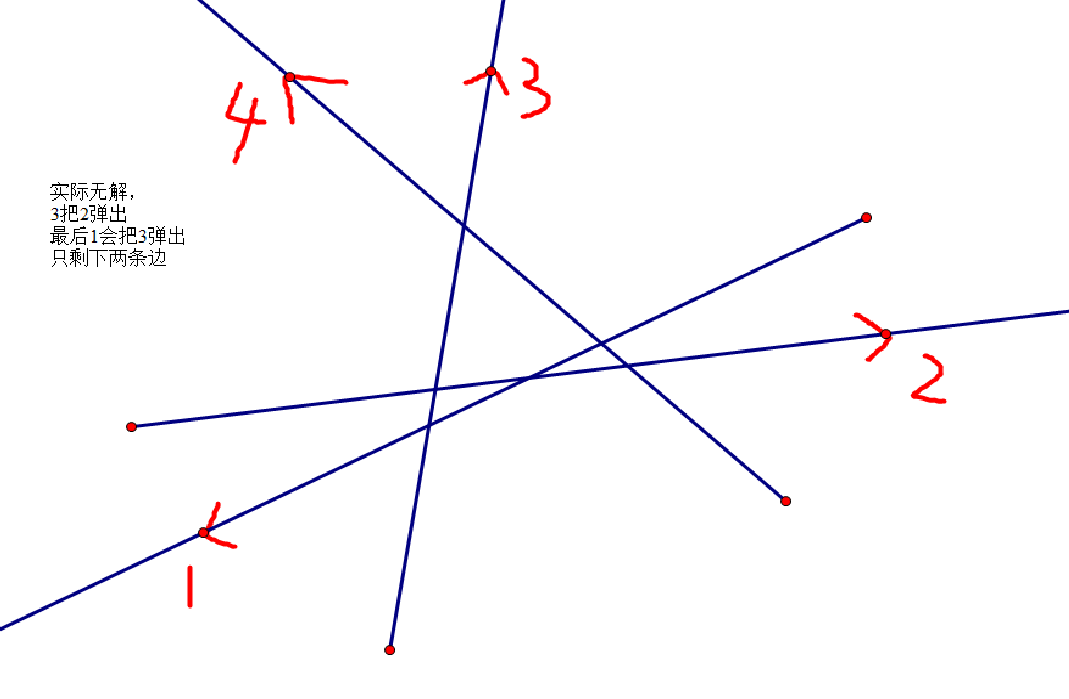
Code:
#include<bits/stdc++.h>
#define maxn 115
using namespace std;
const double eps = 1e-6;
int T,n,m;
double sx[maxn],sy[maxn],sx2[maxn],sy2[maxn];
int sgn(double x){return x>eps?1:x<-eps?-1:0;}
struct Pt{
double x,y;
Pt(double x=0,double y=0):x(x),y(y){}
Pt operator + (const Pt &p)const{return Pt(x+p.x,y+p.y);}
Pt operator - (const Pt &p)const{return Pt(x-p.x,y-p.y);}
Pt operator * (const double &t)const{return Pt(x*t,y*t);}
double operator * (const Pt &p)const{return x*p.y-y*p.x;}
}p[maxn];
struct Line{
Pt p,v; double ang;
Line(Pt p=0,Pt v=0):p(p),v(v),ang(atan2(v.y,v.x)){}
bool operator < (const Line &L)const{return sgn(ang-L.ang)?ang<L.ang:v*(L.p-p)<=0;}
}L[maxn],q[maxn];
int cnt,l,r;
bool Onleft(Pt p,Line L){return L.v*(p-L.p)>0;}
Pt Inter(Line a,Line b){return a.p+a.v*((b.v*(a.p-b.p))/(a.v*b.v));}
double HalfPlane(){
sort(L+1,L+1+cnt);
q[l=r=1]=L[1];
for(int i=2;i<=cnt;i++) if(sgn(L[i].ang-L[i-1].ang)){
while(l<r&&!Onleft(p[r-1],L[i])) r--;
while(l<r&&!Onleft(p[l],L[i])) l++;
q[++r]=L[i],p[r-1]=Inter(q[r-1],q[r]);
}
while(l<r-1&&!Onleft(p[r-1],q[l])) r--;
if(r-l<=1) return 0;
p[r]=Inter(q[l],q[r]);
double ans=0;
for(int i=l;i<=r;i++) ans+=p[i]*p[i+1>r?l:i+1];
return ans/2;
}
int main()
{
scanf("%d",&T);
for(int t=1;t<=T;t++){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) sx[i]=sy[i]=sx2[i]=sy2[i]=0;
for(int i=1,x,y;i<=n;i++) for(int j=1;j<=m;j++){
scanf("%d%d",&x,&y);
sx[i]+=x,sy[i]+=y,sx2[i]+=x*x,sy2[i]+=y*y;
}
printf("Case #%d: ",t);
for(int i=1;i<=n;i++){
L[cnt=1]=Line(Pt(0,0),Pt(1,0)),L[++cnt]=Line(Pt(4095,0),Pt(0,1));
L[++cnt]=Line(Pt(4095,4095),Pt(-1,0)),L[++cnt]=Line(Pt(0,4095),Pt(0,-1));
for(int j=1;j<=n;j++) if(i!=j){
double A=-2*(sx[i]-sx[j]),B=-2*(sy[i]-sy[j]),C=sx2[i]-sx2[j]+sy2[i]-sy2[j];
if(sgn(A)) L[++cnt]=Line(Pt(-C/A,0),Pt(-B,A));
else L[++cnt]=Line(Pt(0,-C/B),Pt(-B,A));
}
printf("%d%c",(int)round(HalfPlane()),i==n?10:32);
}
}
}
![HDU 2036 改革春风吹满地[多边形的面积]](/images/no-images.jpg)

